[Excel] Sommare tariffe giornaliere diverse per data usando le matrici in Excel

Partiamo con uno dei nostri più classici esercizi in Excel. Immaginiamo di avere la seguente tabella di dati, riguardanti i pernottamenti di un gruppo di clienti in un albergo.

Da un’altra parte abbiamo una tabella con le tariffe divise per mese (per comodità abbiamo i mesi già numerati).

A questo punto vogliamo calcolare quanto spenderà ogni cliente sapendo la sua data di ingresso nell’albergo e il numero di pernottamenti. 

La soluzione più banale, sebbene non perfettamente corretta, sarebbe quella di prendere come tariffa di riferimento la tariffa di ingresso e moltiplicarla per il numero di notti. Nel caso specifico nella cella D2 andrebbe la seguente formula:

=CERCA.VERT(MESE(B2);$F$2:$G$13;2;FALSO)*C2

Da questo, applicando la formula su D2:D6, otterremmo un risultato come il seguente:

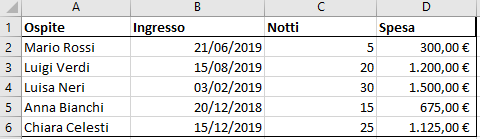
Inutile ribadire come questo risultato non sia corretto, perché in molti casi al passaggio di mese cambia anche la tariffa. Per esempio Chiara Celesti, che comincia il suo soggiorno il 15 dicembre 2019, lo finirebbe l’8 gennaio 2020. Nel caso specifico pagherebbe 45€ per 17 notti e 50€ per 8 notti, per un totale di 1.165€ anziché 1.125€.

Come possiamo quindi risolvere questo problema?

Una possibile soluzione deriva dall’utilizzo delle matrici, con il seguente ragionamento.

Anzitutto spostiamoci in K1 e creiamo la seguente tabella di supporto:

Inseriamo in K2 uno 0, e in K3 la formula  =K2+1  trascinando fino a K42 in modo da ottenere come massimo valore 40. Questo sarà anche il numero massimo di pernottamenti + 1 che potrà fare una persone. Cioè calcoleremo i pernottamenti fino ad un massimo di 41 notti (partendo da 0 fino a 40 compresi). Se volessimo prendere in considerazione più pernottamenti sarebbe sufficiente allungare ulteriormente la formula.

Il ragionamento che voglio fare è il seguente: confrontare l’elenco dei giorni di pernottamento con le date e sovrapporli ad una matrice di costi. Il punto di arrivo è una MATRICE come la seguente:

Figura 1

Questa matrice è riferita ai pernottamenti di Anna Bianchi. Lei comincia la vacanza il 20 dicembre e la finisce il 3 gennaio. Significa che copre 12 giorni di dicembre e 3 di gennaio. Usando la matrice di K2:K42 sommiamo alla data di partenza da 0 fino a n giorni, ovvero da 0 a 14 giorni, arrivando così ad avere tutte le date dal 20 dicembre al 3 gennaio.

Rispetto alla matrice precedente avremmo una tabella come quella che segue:

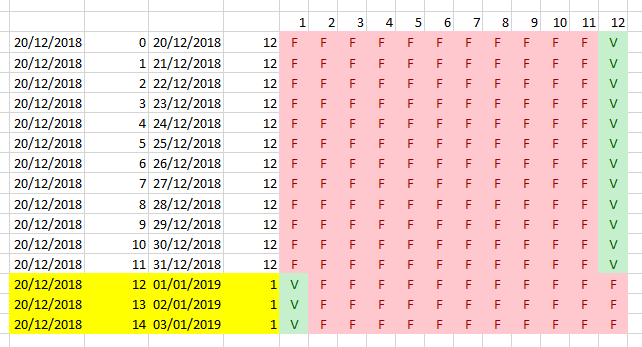
Figura 2

Nella prima colonna abbiamo la data di ingresso ripetuta su tutta la durata, nella seconda colonna abbiamo i giorni da 0 a 14, fino cioè a 15 escluso (che è il numero di pernottamenti). Se sommiamo alla data di ingresso ciascun giorno otteniamo le relative date di pernottamento. Usando la funzione MESE() su ciascuna data otteniamo quindi la quarta colonna con la codifica del mese. Infine eguagliamo la colonna dei mesi di pernottamento con la riga di tutti i mesi, ottenendo la matrice di uguaglianze (vero e falso) come di sopra.

Fatto questo andremo a prendere una matrice di prezzi fatta nel modo seguente:

Figura 3

Sovrapponendo le due matrici, solo dove nella prima abbiamo VERO otterremo una matrice così:

Figura 4

Ai FALSO abbiamo sostituito uno 0. A questo punto vediamo che facendo un SOMMA() su questa matrice possiamo calcolare esattamente la tariffa che dovrà pagare Anna Bianchi.

Per realizzare tutto questo con una singola formula utilizzeremo le MATRICI di Excel nel modo seguente.

Anzitutto otteniamo la prima colonna dei mesi come nella Figura 1 utilizzando la seguente formula:

=MESE(B2+$K$2:$K$42)

Se premiamo F9 sulla formula evidenziata dovremmo vedere una matrice come la seguente per il primo caso (quello del 21 giugno 2019)

{6.6.6.6.6.6.6.6.6.6.7.7.7.7.7.7.7.7.7.7.7.7.7.7.7.7.7.7.7.7.7.7.7.7.7.7.7.7.7.7.7}

Qui vediamo che vengono calcolati tutti i mesi per i prossimi 40 giorni a partire dalla data di partenza, mentre Mario Rossi rimane solo per 5 giorni. Vogliamo quindi a 0 i giorni superflui e integriamo con la seguente formula:

=SE($K$2:$K$42<C2;MESE(B2+$K$2:$K$42);0)

Il risultato diventerà:

{6.6.6.6.6.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0}

Così abbiamo ottenuto la colonna dei mesi della Figura 1. Per ottenere la matrice la eguagliamo ai mesi in F2:F13, siccome però vogliamo ottenere una matrice rettangolare dobbiamo eguagliarli ad una matrice riga, mentre F2:F13 è una matrice colonna. A tale proposito useremo la funzione MATR.TRASPOSTA() che traspone una matrice colonna in una matrice riga.

=SE($K$2:$K$42<C2;MESE(B2+$K$2:$K$42);0)=MATR.TRASPOSTA($F$2:$F$13)

Ancora F9 e otteniamo:

{FALSO\FALSO\FALSO\FALSO\FALSO\VERO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\VERO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\VERO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\VERO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\VERO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO.FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO\FALSO}

In questo ginepraio di FALSO possiamo notare alcuni VERO all’inizio, in corrispondenza con il mese in colonna e quello in riga.

A questo punto usiamo il SE nel modo per cui se nella matrice c’è un VERO allora prendi il prezzo dalla matrice dei prezzi, simile a quella della Figura 3 che creiamo usando:

=MATR.PRODOTTO($L$2:$L$42;MATR.TRASPOSTA($G$2:$G$13))

Questa particolare operazione darebbe infatti questo risultato:

{50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45.50\50\55\55\55\60\60\60\50\50\45\45}

Uniamo le due cose nel modo seguente:

=SE(SE($K$2:$K$42<C2;MESE(B2+$K$2:$K$42);0)=MATR.TRASPOSTA($F$2:$F$13);MATR.PRODOTTO($L$2:$L$42;MATR.TRASPOSTA($G$2:$G$13));0)

Questa formula darebbe (sempre usando F9):

{0\0\0\0\0\60\0\0\0\0\0\0.0\0\0\0\0\60\0\0\0\0\0\0.0\0\0\0\0\60\0\0\0\0\0\0.0\0\0\0\0\60\0\0\0\0\0\0.0\0\0\0\0\60\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0.0\0\0\0\0\0\0\0\0\0\0\0}

Da notare come compaiono esattamente 5 numeri 60, corrispondenti alla tariffa di giugno che deve pagare Mario Rossi.

Applichiamo a questa matrice la funzione SOMMA() e premiamo SHIFT+CTRL+INVIO per applicare il calcolo matriciale al risultato.

La formula finale sarà:

=SOMMA(SE(SE($K$2:$K$42<C2;MESE(B2+$K$2:$K$42);0)=MATR.TRASPOSTA($F$2:$F$13);MATR.PRODOTTO($L$2:$L$42;MATR.TRASPOSTA($G$2:$G$13));0))

E dovremmo vedere qualcosa di simile nel nostro foglio:

Se abbiamo fatto tutto bene il numero risultato sarà dunque:

Con i valori corretti per ogni cliente su qualunque pernottamento.