L’articolo Paradosso di Monty Hall spiegato con Excel, è per te che sei tanto incuriosito quanto scettico circa questo bizzarro gioco, e del perché si abbia a che fare con delle Capre ed un’Auto di lusso. Premetto che sarebbe più corretto chimarlo Problema di Monty Hall e non Paradosso, ma visto che oramai è diffuso come Paradosso… che tale sia!
Quello che forse stai cercando è un semplice file di Excel, che, anche senza essere un programmatore possa, “numeri alla mano” convincerti che le probabilità a cui il paradosso si riferisce sono effettivamente corrette.
Il mio desiderio è che questo tutorial possa esserti di aiuto in modo corretto e semplice. Se hai dei dubbi o perplessità circa alcuni passaggi esposti, sentiti libero di contattarmi. Alla fine dell’articolo troverai i miei contatti.
Paradosso di Monty Hall spiegato con Excel – Nascondiamo le Capre e l’Auto!
Vediamo adesso come costruire il foglio di calcolo che ci consenta di “toccare con mano” l’esperimento:
- Scarica il file “Monty_Hall_Vuoto.xlsx” che ti consentirà di iniziare subito lo svolgimento

L’immagine si ferma alla riga 15, ma la verifica empirica eseguirà un test su 1000 scommesse.
- Nella riga 4 identifica STEP1.
- Nella cella A6 scrivi la formula che segue:
- =CERCA.VERT(CASUALE.TRA(1;3);$T$5:$U$7;2;0)
- La formula estrae un numero intero compreso tra 1 e 3 e lo converte in Capra o Auto come da Tavola di Allocazione indicata al suo interno.
- Nella cella B6 scrivi la formula
- =SE(A6<>”Auto”;CERCA.VERT(CASUALE.TRA(1;2);$T$5:$U$6;2;0);”Capra”)
- Se nella conversione casuale precedente non si è generato il valore “Auto” allora si effettua una nuova conversione casuale, ma questa volta con l’estrazione di soli due valori interi, compresi tra 1 due convertiti rispettivamente in “Capra” ed “Auto”.
- Se né al punto 2 e 3, si è allocata l’auto, lo faremo con la formula che segue, da depositare nella cella C6:
- =SE(CONTA.SE(A6:B6;”Auto”)=0;”Auto”;”Capra”)
- Copiamo ed incolliamo le formule fino alla riga 1005
- Otterrai qualcosa di simile a quanto segue, ma ricorda che i valori sono casuali e che quindi il prospetto che ricaverai non potrà essere uguale a quello che segue

- Nello STEP 2 lasceremo che il giocatore effettui la sua scommessa, scrivendo su una delle tre porte la parola “Scelta!”
- Nella cella D6 scrivi la seguente formula
- =CERCA.VERT(CASUALE.TRA(1;3);$T$5:$V$7;3;0)
- La formula converte tre numeri interi generati casualmente tra 1 e 3 in una sola “Scelta!” e due celle vuote
- In tal proposito, le celle V6 e V7 ospitano la formula che segue:
- =””
- Diversamente il CERCA.VERT restituirebbe un valore pari a zero
- Nella cella E6 scrivere la formula che segue
- =SE(D6=”Scelta!”;””;CERCA.VERT(CASUALE.TRA(1;2);$T$5:$V$6;3;0))
- In sostanza se al passaggio 8 abbiamo generato la “Scelta!” lasceremo la cella vuota, diversamente riproponiamo la conversione casuale tra due valori soltanto, rimanendo due celle da riempire
- Nella cella F6 scrivere la seguente formula:
- =SE(CONTA.SE(D6:E6;”Scelta!”)=0;”Scelta!”;””)
- Se nei passaggi 8 e 9 non è stata generata la scelta, lo facciamo adesso, altrimenti lasciamo la cella vuota.
- Ricopia le formule fino alla riga 1005 e ricorda che i valori cambieranno ad ogni modifica del foglio

Paradosso di Monty Hall spiegato con Excel. Scegliamo la porta!
- STEP 3. È arrivato il momento di entrare nei panni del conduttore del gioco. Ricordiamo che il conduttore conosce la posizione dell’Auto e la scelta fatta dal giocatore.
- Abbiamo a disposizione tre porte. Apriremo una porta che il giocatore non ha scelto e che contiene una “Capra”
- Prima porta. Il conduttore decide se aprirla
- Prima di aprire la porta ci assicuriamo che non sial quella “Scelta!” e che dietro non ci sia l’”Auto”
- Nella cella G6 scrivere la seguente formula:
- =SE(E(D6<>”Scelta!”;A6<>”Auto”);A6;””)
- Certamente sarà visualizzata solo la parola “Capra”
- Seconda Porta.
- Nella cella H6 ripetiamo il ragionamento effettuato solo se non abbiamo aperto già la porta con la “Capra”. Ecco perché scriveremo la formala che segue:
- =SE(E(G6=””;B6<>”Auto”;E6<>”Scelta!”);B6;””)
- Siamo alla Terza Porta.
- Apriremo la porta numero tre, soltanto se non abbiamo aperto una delle due precedenti e se non nasconde l’”Auto” dietro di sé. Ecco che in cella I6 scriveremo:
- =SE(E(G6=””;H6=””;C6<>”Auto”);C6;””)
- Ricopiamo le formule fino alla riga 1005. Ricordiamo che i valori cambieranno e che quindi la figura che segue è soltanto indicativa

- Entriamo adesso nel vivo del gioco
Scenario primo: il giocatore non cambia la scelta. Paradosso di Monty Hall spiegato con Excel
- Dopo aver aperto la porta che il giocatore non ha scelto e che nascondeva una capra, gli si concede la possibilità di cambiare la scelta iniziale. Egli non accetta e CONFERMA quanto già scelto
- Nelle colonne J, K ed L, sintetizziamo in un unico prospetto lo Step 2 e lo Step 3.
- Sulla stessa riga, avremo quindi la porta “Scelta!” e la porta aperta con la “Capra”.
- Nella cella J6 scriviamo quindi la formula che segue:
- =SE(D6<>”Scelta!”;G6;D6)
- Nella cella K6 scriviamo la seguente formula:
- =SE(E6<>”Scelta!”;H6;E6)
- Nella cella L6 scriviamo la seguente formula:
- =SE(F6<>”Scelta!”;I6;F6)
- Ricopiamo le formule fino alla riga 1005. Ricordiamo che i valori cambieranno e che quindi la figura che segue è soltanto indicativa
- Mediante la formattazione condizionale sono state evidenziate di arancione le scelte vincenti. Tutte le celle non vincente, per contro, sono grigio scuro.
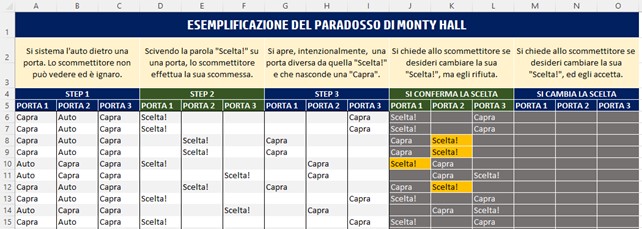
- Alla fine del tutorial saranno esposte le formule relative alla formattazione condizione
Scenario due: Il giocatore cambia la scelta. Paradosso di Monty Hall spiegato con Excel
- Dopo aver aperto la porta che il giocatore non ha scelto e che nascondeva una “Capra”, gli si concede la possibilità di cambiare la scelta iniziale. Egli ACCETTA cancellando la scritta di “Scelta!” sulla porta scelta in precedenza e riscrivendola sull’unica porta chiusa diversa dalla prima scelta
- Nella cella M6 scrivere la seguente formula:
- =SE(G6=”Capra”;”Capra”;SE(E(D6<>”Scelta!”;G6<>”Capra”);”Scelta!”;””))
- Nella cella N6 scrivere la seguente formula:
- =SE(H6=”Capra”;”Capra”;SE(E(M6<>”Scelta!”;E6<>”Scelta!”;H6<>”Capra”);”Scelta!”;””))
- Nella cella O6 scrivere la seguente formula:
- =SE(I6=”Capra”;”Capra”;SE(E(M6<>”Scelta!”;N6<>”Scelta!”;F6<>”Scelta!”;I6<>”Capra”);”Scelta!”;””))
- Ricopiamo le formule fino alla riga 1005. Ricordiamo che i valori cambieranno e che quindi la figura che segue è soltanto indicativa
- Mediante la formattazione condizionale sono state evidenziate di verde le scelte vincenti. Tutte le celle non vincenti, per contro, sono grigio scuro.
- Alla fine del tutorial saranno esposte le formule relative alla formattazione condizione
- Ricopiamo le formule fino alla riga 1005. Ricordiamo che i valori cambieranno e che quindi la figura che segue è soltanto indicativa
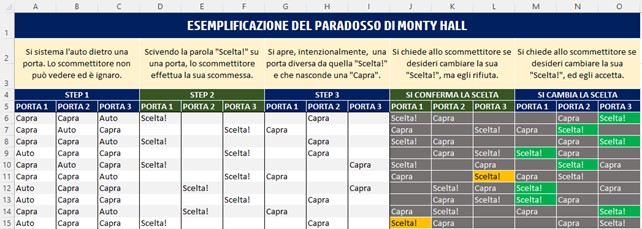
- Mediante la formattazione condizionale sono state evidenziate di verde le scelte vincenti. Tutte le celle non vincenti, per contro, sono grigio scuro.
- Alla fine del tutorial saranno esposte le formule relative alla formattazione condizione
Confronto degli scenari. Paradosso di Monty Hall spiegato con Excel
- Con un prodotto tra due matrici, andremo a generare una matrice di 1 e 0. Gli uno rappresentano le scelte vincenti, mentre gli zero rappresentano le scelte perdenti
- La Somma degli 1 disponibili sarà in grado di dirci il numero di vittorie per entrambi gli scenari, rendendo possibile il confronto.
- Nella cella Q5 scriviamo la formula che segue, convalidandola con CTRL+SHIFT+INVIO:
- =SOMMA(SE(A6:C1005=”Auto”;1;0)*SE(J6:L1005=”Scelta!”;1;0))
- Nella cella R5 scriviamo la formula che segue convalidandola con CTRL+SHIFT+INVIO:
- =SOMMA(SE(A6:C1005=”Auto”;1;0)*SE(M6:O1005=”Scelta!”;1;0))
- Nella cella Q6 scriviamo la seguente formula:
- =Q5/(Q5+R5)
- Nella cella R6 scriviamo la seguente formula:
- =R5/(Q5+R5)
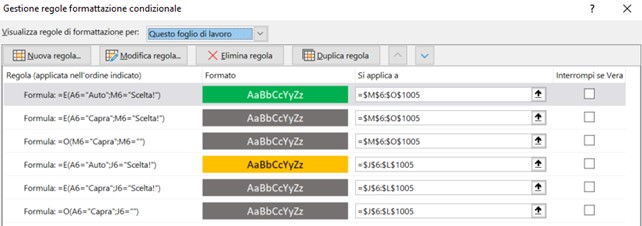
Formattazione Condizionale.
- Per quanto riguarda la formattazione condizionale si consideri la seguente immagine
Conclusioni.
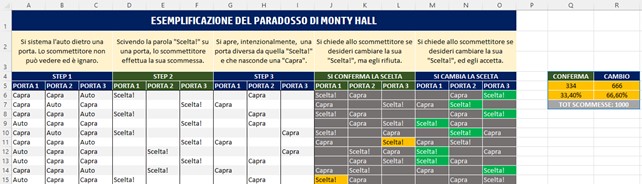
Osservando il piccolo prospetto di riepilogo delle vittorio registrate nei due scenari, si comprende facilmente che conviene cambiare scelta se, date le regole del gioco stabilite inizialmente, ci viene data la possibilità di cambiare la scelta.
Da un punto di vista probabilistico, quando si inizia il gioco ciascuna porta ha le stesse probabilità di vincere e cioè una su tre, pari al 33,33%.
Quando si sceglie una porta si ha quindi il 33,33% di vincere. Le due porte “non scelte” rappresentano il 66,66% di probabilità di vittoria.
Nel momento in cui una delle due porte “non scelte” viene aperta e si dimostra perdente, il 66,66% delle probabilità di vittoria iniziale delle porte “non scelte” si concentra sull’unica porta “non scelta” rimasta.
La porta scelta continua ad avere il 33,33% di probabilità di vittoria, mentre quella rimasta delle due “non scelte” concentra su di sé il 66,66% di probabilità di essere vincente.
Da quanto esposto si ha un’ulteriore conferma circa la migliore opportunità di vincita rappresentata da un cambio di scelta.
Per scaricare il file completo clicca qui. Se lo ritieni opportuno utilizzalo pure, ti chiedo di riconoscermi il credito 🙂
Se desideri scoprire di più!
L’articolo è scritto da Gabriele di Ruvo, docente di analisi dei Dati per Mummu Academy e molte altre realtà aziendali.
Gabriele e la sua azienda sono disponibili per stage e formazione sia on-site che a distanza sia per i privati che per le aziende che desiderano migliorare le proprie competenze nella Data Analysis.
Nella formazione a distanza, sincrona ed asincrona, Mummu Academy mette a disposizione la propria piattaforma di E-Learning.
Se sei interessato puoi contattare direttamente Mummu Academy allo 055 4223105 o scrivere a g.diruvo@mummuacademy.it.
Potrebbe interessarti anche
Se hai trovato interessante questo articolo, potrebbero piacerti anche i seguenti:
[EXCEL] Funzione DATA.DIFF: differenze tra date in Anni, Mesi e Giorni
[Excel] Sommare tariffe giornaliere diverse per data usando le matrici in Excel
Molti altri ancora nel mio blog in Mummu Academy



