Utilizzo Del Risolutore Di Excel
Immaginiamo di dover posizionare Cinque Distributori di bevande idonei a servire 25 Campi da Tennis di un magnifico centro sportivo.
Possiamo decidere di ubicarli dove desideriamo, ma il nostro scopo è il seguente:
- Attribuire a ciascun campo da tennis un apposito distributore in modo che lo spostamento dei giocatori sia il minimo possibile quando escono dal campo per recarsi al distributore.
Prepariamo Il “Campo Da Gioco”
- Per prima cosa dobbiamo immaginare di distribuire su di un Piano Cartesiano, in modo del tutto casuale i 25 campi da tennis
- Lo facciamo assegnando delle coordinate X ed Y comprese tra 0 e 100. In questo modo sappiamo che ipoteticamente ogni asse di allocazione ha un valore minimo di 0 e massimo di 100. Abbiamo identificato il perimetro virtuale del nostro centro sportivo.
- Nel prospetto che segue ho utilizzato la funzione =CASUALE.TRA(0;100) per generare le coordina te X,Y. Subito dopo ho reso statistici i valori con un Copia-Incolla Valori.
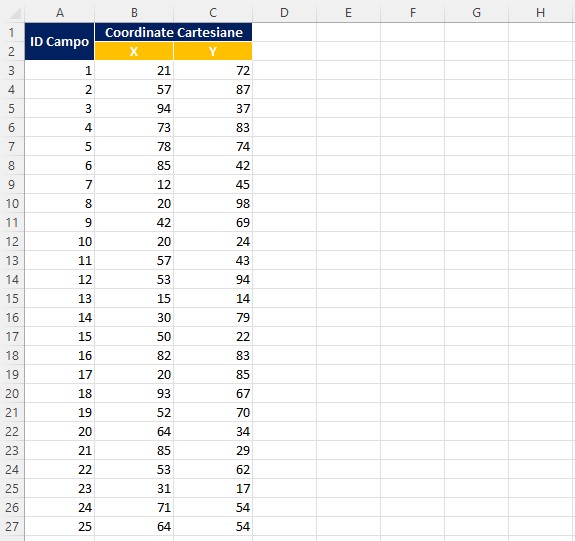
- Clicca qui per scaricare il file dell’immagine sopra.
Assegniamo Ai Campi I Distributori Di Bevande
- Prepariamo adesso una colonna in cui si assegna a ciascun campo il relativo ID distributore.
- Prima di usare l’algoritmo di assegnazione e solo per comodità assegneremo a tutti i campi lo stesso ID Distributore e cioè il numero 1.
- Si ha quindi che
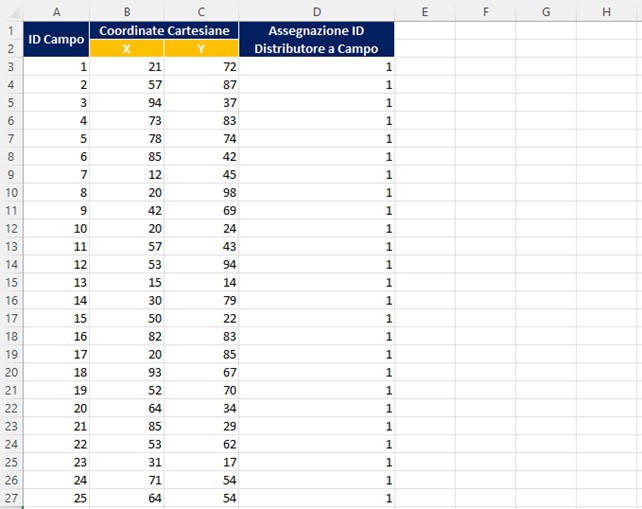
Posizioniamo I Distributori di Bevande
- Posizioniamo adesso i cinque distributori di bevande.
- Inizialmente li metteremo tutti nello stesso punto con coordinate X,Y pari a 0,0.
- Più avanti, useremo il “Risolutore” per ottenere le coordinate definitive.
- Possiamo adesso calcolare la distanza tra i campi da tennis ed i distributori utilizzando il teorema di pitagora ed i punti sul piano cartesiano.
- Vediamo di seguito un esempio che possa chiarire il concetto
- Immaginiamo di avere due punti:
- Punto A
- Punto B
- Di seguito vengono riportate le coordinate di entrambi i punti
- Posizioniamo i punti all’interno di un grafico
- Immaginiamo di dover calcolare la loro distanza
- Seguo lo sviluppo del ragionamento nella figura che segue
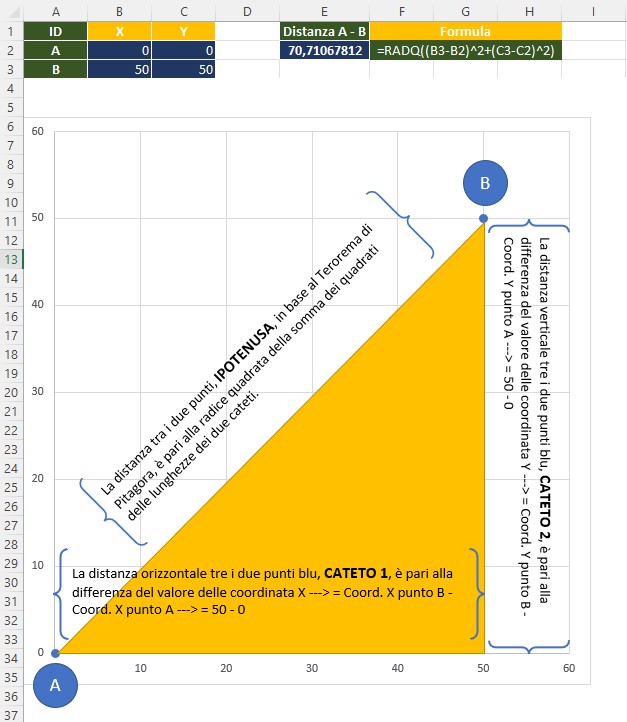
- Adesso si va incontro alla parte più delicata del tutorial che è quella relativa alla formula atta al calcolo della distanza tra i due punti presenti nel foglio dell’esercizio.
- Il problema è che avendo da gestire 5 distributori, il loro posizionamento per quanto riguarda gli assi X e Y cambia in base al valore assegnato lungo il Range D3:D27.
- Nel Range D3:D27, infatti per ciascuna cella è possibile un valore intero che va da 1 a 5.
- In base al numero che si sceglie, si deve prendere la corrispondente coppia di coordinate X,Y presente nell’Array H3:I7
- In questo senso ci aiuta molto la formula SCARTO che, da una origine, è in grado di prendere il valore che si trova in una posizione di OFFSET.
- Nel nostro caso lo scarto è soltanto in verticale e non in orizzontale.
- Per meglio comprendere la funzione si rimanda al seguente link ufficiale
- In base a quanto illustrato avremo la seguente formula nella cella E3
- =RADQ((B3-SCARTO($H$2;D3;0))^2+(C3-SCARTO($I$2;D3;0))^2)
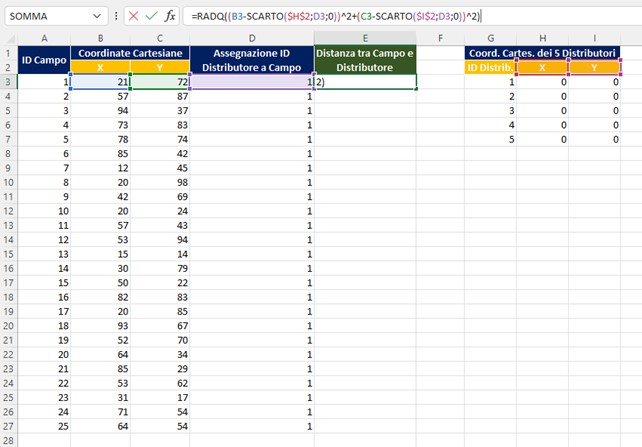
- L’algoritmo dovrà minimizzare la somma della distanza totale ottenuta sommando i valori del range E3:E27.
- Appare evidente che la simulazione dovrà testare cosa accade mischiando tra di loro innumerevoli soluzioni di ID deposito per ciascuna riga.
- Il range D3:D27 verrà popolato con milioni e milioni di valori generati dal risolutore, tutti compresi tra 1 e 5.
- L’allocazione ottimale è quella con la quale si ottiene il valore di somma totale delle distanze più piccolo possibile.
- Le coordinate assegnate ai distributori di bevande dovranno rientrare all’interno del perimetro illustrato nel range K1:M4
Obiettivo, Variabili e Vincoli
- In sostanza abbiamo il seguente obiettivo e le seguenti variabili fa gestire entro specifici vincoli:
- Obiettivo —> Minimizzare il valore della cella £28
- Modificando le seguenti celle variabili —> H3:I7
- Modificando le seguenti celle variabili —> D3:D27 —> devono essere comprese tra 1 e 5 ed Intere
- Vincolo per X —> H3:H7 >= L3
- Vincolo per X —> H3:H7 <= M3
- Vincolo per Y —> I3:I7 >= L4
- Vincolo per Y —> I3:I7 <= M4
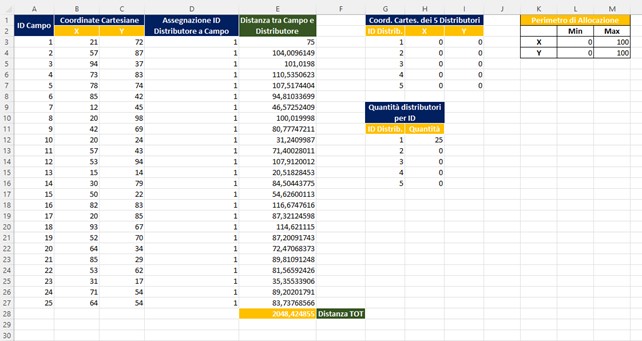
- Prima di chiedere al Risolutore di entrare in azione inseriamo un calcolo di quanti distributori vengono assegnati per ID —> vedi range G9:H16
- La formula per il conteggio è le seguente per la cella H12 —> =CONTA.SE($D$3:$D$27;G12)
- Si ha che
Prepariamo Il Grafico
Vediamo la configurazione anche da un punto di vista grafico.
Seguiamo la seguente procedura:
- Selezioniamo il range B3:C27
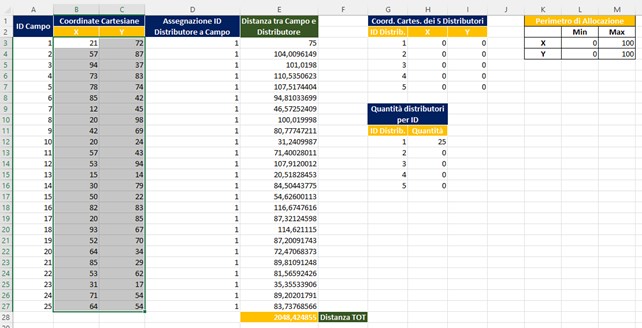
- Inseriamo grafico a dispersione X,Y
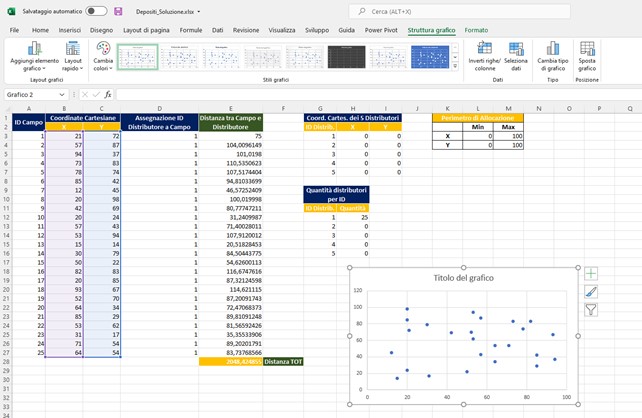
- Tasto DX su Grafico
- Seleziona Dati
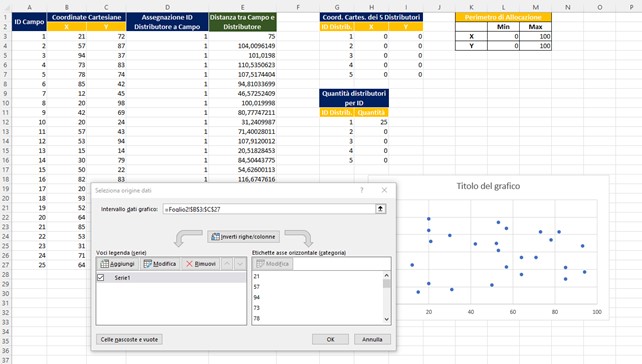
- Aggiungi
- Imposto come da figura
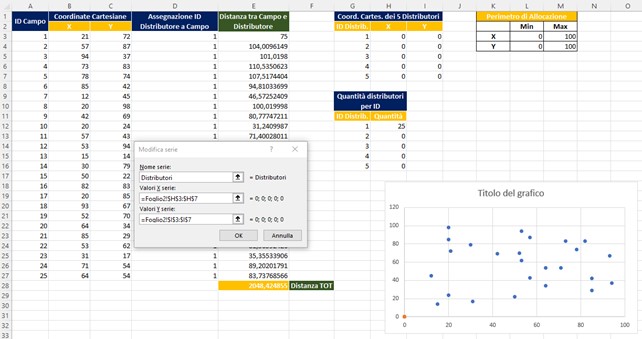
- Si ha che
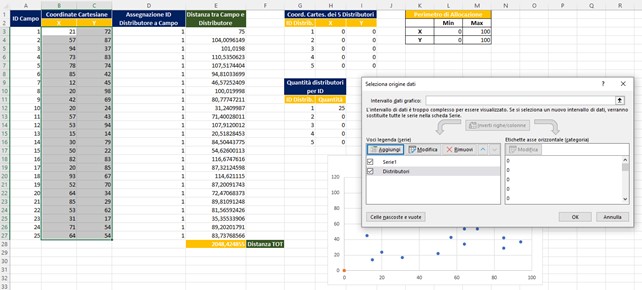
- Rinomino Serie1 —> Campi
- Si ha che
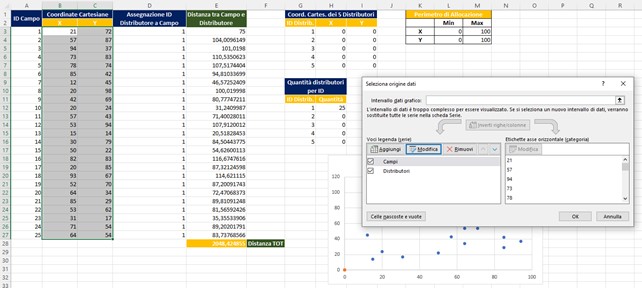
- Modifico grafico come segue
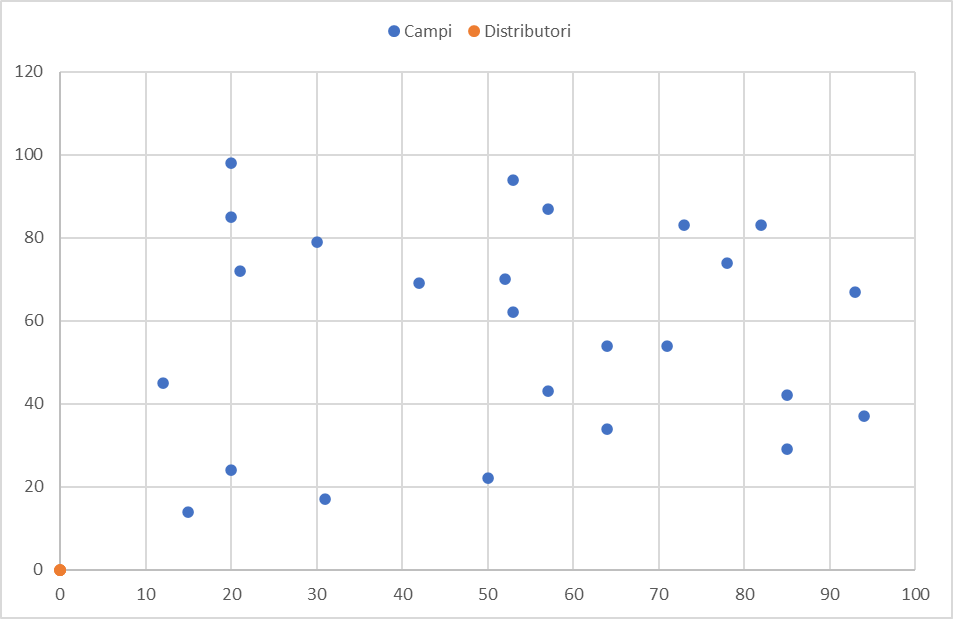
- I distributori sono tutti posizionati alle origini degli assi, ma poi si sposteranno in base ai dati identificati dall’algoritmo.
- A questo punto aziono dalla scheda dati il Risolutore.
Abilitiamo Il Tool Risolutore
- Per chi non avesse ancora attivato e reso disponibile il relativo menu: fai click qui
- Imposto il risolutore come da figura
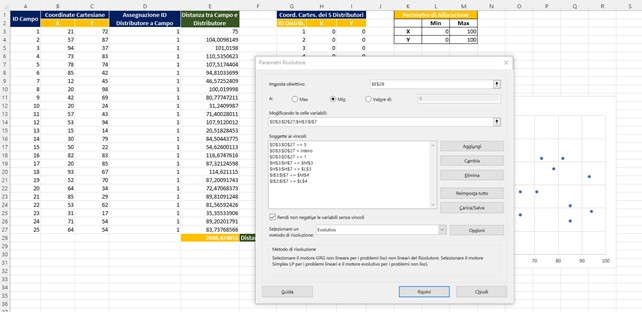
- Premendo Risolvi Excel inizia i suoi calcoli che potranno durare anche qualche minuto: dipende moltissimo dalla potenza del PC che si usa
- Alla fine del processo di calcolo Excel ci propone delle soluzioni
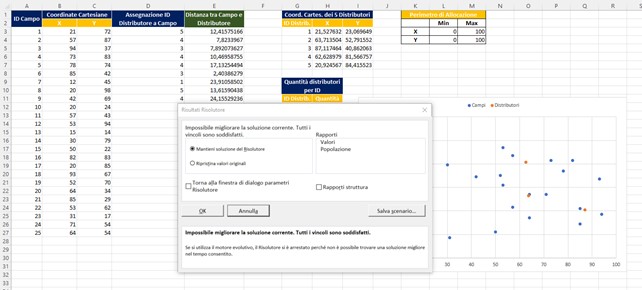
- Anche prima di premere accetta possiamo vedere che i punti arancioni sono adesso sparsi nel perimetro designato.
- Premiamo OK
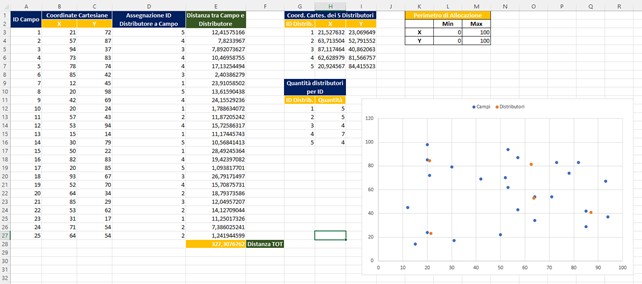
- Da cui
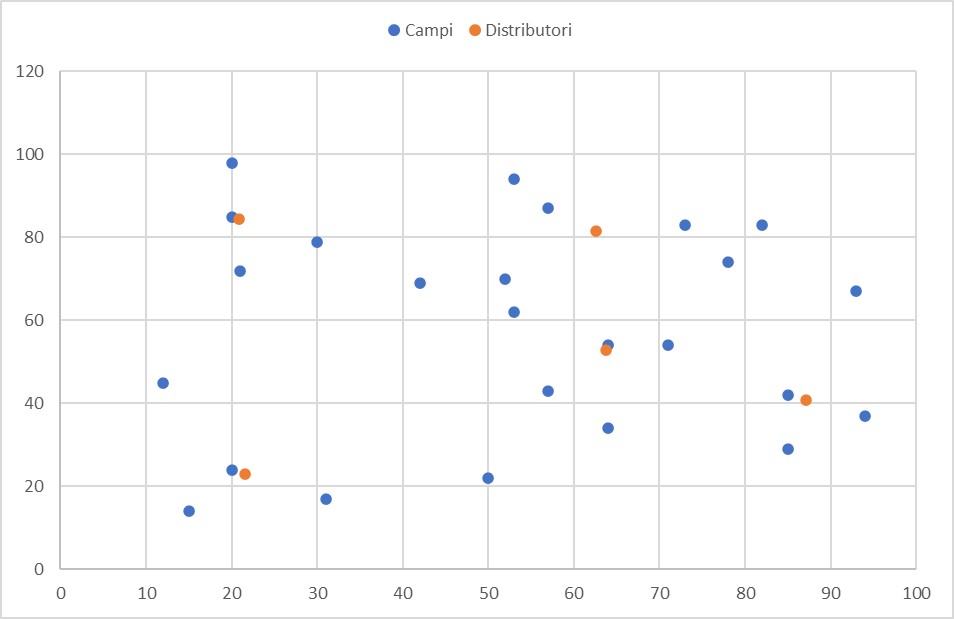
- Non aspettiamoci che Excel trovi la stessa soluzione ad ogni tentativo.
- I risultati possono variare di qualche unità dopo ogni simulazione. Questo dipende dal tipo di algoritmo che il risolutore usa nei calcoli.
- Se mi hai seguito fin qui ti meriti il download della soluzione completa: clicca qui per scaricare tutto il file svolto.


