A chi non è capitato di dover sintetizzare, con un unico valore, una serie di valori? Quale indice scegliere? Media Varianza e Deviazione Standard sono idonei?
Prima o poi tutti ci imbattiamo in questa esigenza e la soluzione che più spesso viene utilizzata è calcolare la MEDIA ARITMETICA.
La MEDIA, in realtà non è in grado di darci un’idea di come i valori siano distribuiti intorno ad essa stessa. Un brevissimo esempio può aiutarci a capire meglio.
Immaginiamo che due persone svolgano nel tempo 10 compiti scritti ciascuno e che la loro media dei voti sia pari a 6. Siamo in grado, disponendo della sola media, di definire il loro rendimento nel tempo? La risposta è no: il primo studente potrebbe avere 6 come media perché ha preso un voto pari a 6 per ciascun compito, mentre il secondo potrebbe aver preso delle insufficienze alternate a degli ottimi voti.
Con l’esempio precedente percepiamo il limite di un indice di posizione centrale quale la MEDIA.
Per fortuna esistono gli indici di dispersione quali la VARIANZA e la DEVIAZIONE STANDARD che sono in grado di superare il limite appena identificato. Tali indici ci danno un precisa valutazione di come gli indici siano distribuiti intorno alla MEDIA della distribuzione a cui appartengono.
VARIANZA E DEVIAZIONE STANDARD: PRIMI PASSI
Passiamo adesso all’azione con un esercizio guidato che usi Excel come strumento per capire davvero come stiano le cose.
Utilizziamo adesso il Data-set disponibile a questo link: su ogni riga si hanno i risultati di giocatori diversi su cinque gare da loro disputate.

Nella figura abbiamo già calcolato la MEDIA, la MEDIANA e la MODA, anche se per adesso utilizzeremo la MEDIA.

VARIANZA E DEVIAZIONE STANDARD: GLI SCARTI DALLA MEDIA
Dal momento che desideriamo conoscere come i dati si distribuiscono intorno alla MEDIA, per ciascuno di essi, calcoliamo il relativo SCARTO DALLA MEDIA:

Notiamo che la SOMMA DEGLI SCARTI è pari a zero, sperimentando in modo pratico una delle principali proprietà della MEDIA.
In realtà la somma degli scarti pari a zero, ci dà qualche problema nel momento in cui desiderassimo calcolare la MEDIA DEGLI SCARTI. Il numeratore della formula, infatti, andrebbe zero per qualsiasi distribuzione.
Capiamo adesso perché nel prossimo passaggio eleveremo a quadrato ogni scarto: sicuramente saranno valori positivi.
VARIANZA E DEVIAZIONE STANDARD: GLI SCARTI AL QUADRATO

La SOMMA DEGLI SCARTI AL QUADRATO non è pari a zero a meno che tutti gli scarti siano zero.
LA MEDIA DEGLI SCARTI AL QUADRATO
Calcolo adesso la MEDIA DEGLI SCARTI AL QUADRATO: divido la loro somma per il numero dei partecipanti alla gara di riferimento:

Nel passaggio precedente abbiamo scoperto la VARIANZA delle distribuzione esaminate.
Adesso, a posteriori, vediamo quale sia la formula che ne sintetizza i passaggi:

Al numeratore abbiamo la sommatoria degli scarti, mentre al denominatore il loro numero totale.
La VARIANZA ha tuttavia una scala diversa da quella dei numeri originari in quanto deriva da un elevamento al quadrato. Capiamo perché ne calcoliamo la radice quadrata, ottenendo la DEVIAZIONE STANDARD o SCARTO QUADRATICO MEDIO:
LA RADICE QUADRATA DELLA VARIANZA
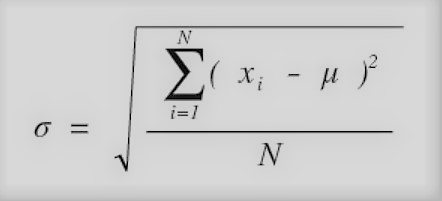
Di seguito i valori ed i loro indici per ciascuna delle singole serie:

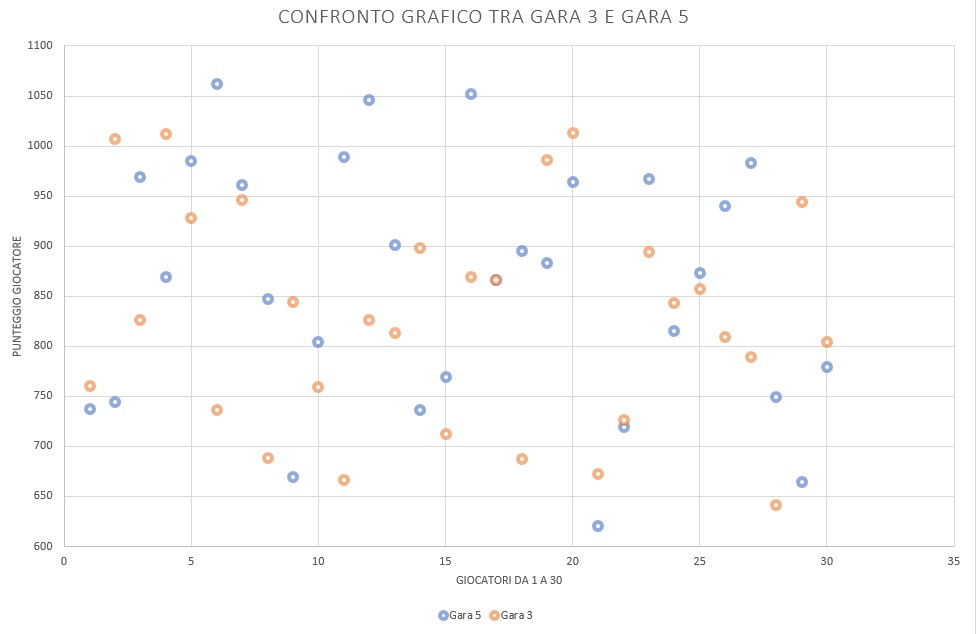
Se osserviamo la DEVIAZIONE STANDARD notiamo che esiste un bel divario tra la terza serie e la quinta. Cosa significa?
La terza serie, avendo una DEVIAZIONE STANDARD più bassa sarà quella i cui valori sono più schiacciati intorno alla media, soprattutto nei confronti della quinta che ha il valore più alto.
In questo tutorial non abbiamo utilizzato intenzionalmente le formule che in Excel permettono il calcolo diretto della Varianza e della Deviazione Standard. Lo scopo era quello di spiegare passaggio dopo passaggio il loro significato con l’aiuto di Excel.
Se sei interessato a questi argomenti potresti trovare utile il nostro corso per un UTILIZZO AVANZATO DI EXCEL. Tieni presente che i principali indici statistici sono molto utili anche per chi intende utilizzare al meglio i SOCIAL per promuovere la propria attività.


