Davanti ad un report stracolmo di dati, anche se ben elencati e categorizzati, non è semplice raccogliere delle informazioni. Dato ed informazione sono due concetti con numerose intersezioni, ma con molte differenze. Il dato, di per sé non è detto che rappresenti un’informazione. Potrebbe, infatti, essere rappresentativo di determinazioni non pertinenti alla mia analisi oppure non essere aggregato in una forma di sintesi idonea.
La STATISTICA DESCRITTIVA è un ottimo alleato per raggiungere il nostro scopo. Esaminiamo adesso in modo semplice alcuni basilari indici di posizione che la Statistica descrittiva ci offre.
Cerchiamo di essere più chiari con un semplice esempio. Se esportassi dal mio gestionale un lungo elenco di prodotti venduti con le relative quantità avrei soltanto dei dati. Se riuscissi ad aggregare gli stessi, ottenendo il numero di volte che li ho venduti in un determinato periodo e identificando anche le relative quantità vendute, avrei quelle che per me sarebbero delle informazioni sulle vendite. Esercitiamoci con la figura di seguito riportata.
Cliccando qui potrai effettuare il download del file.
In questo esempio abbiamo dei record relativi alle vendite di occhiali. Proviamo ad allenarci i più usati INDICI DI POSIZIONE DI BASE della statistica descrittiva. Notiamo che in questo esempio trattiamo dei dati che non sono raggruppati in classi di appartenenza. Tratteremo gli indici di posizione per dati raggruppati per classi in un apposito articolo.
MEDIA ARITMETICA
Si tratta del valore di posizione più utilizzato. Dato un insieme di “n” elementi, la media aritmetica, utilizzata per le variabili quantitative, è quel valore che sostituito nella somma degli “n” elementi lascia invariato il risultato finale. Nell’esempio riportato nella figura, la media aritmetica è rappresentata dalla somma dei valori delle determinazioni divise per il numero univo degli elementi stessi. La più immediata applicazione di questo indice nel nostro esempio è il calcolo della media aritmetica dell’importo delle vendite. Sono state eseguite “n” vendite dove n=24. Il numero di occhiali venduti è infatti pari a 24. La somma delle “n” determinazioni è pari ad € 2.886,00. La media aritmetica è facilmente determinabile dividendo l’importo di € 2.886,00 per 24, ottenendo come risultato un valore pari ad € 119,42
In Excel è sufficiente individuare la serie di valori di cui si desidera la MEDIA ARITMETICA utilizzando la seguente funzione:
=MEDIA(E2:E25) il cui risultato è pari ad € 119,42
Proviamo adesso a verificare il risultato identificando con altre formule i singoli fattori. Per determinare il numero degli elementi di cui desideriamo la media utilizziamo una semplice funzione di conteggio:
=CONTA.NUMERI(E2:E25) il cui risultato è pari a 24
Si tratta di una funzione che conteggia il numero di volte che in un intervallo di celle il loro contenuto è rappresentato da dei numeri
Utilizzerò la funzione di SOMMA per ottenere la somma delle “n” determinazioni appartenenti all’insieme dei valori di cui desideriamo calcolare la media
=SOMMA(E2:E25) il cui risultato è pari ad € 2.886,00
La funzione che indica quanti valori numerici appartengono all’insieme è invece la seguente:
=CONTA.NUMERI(E2:E25) il cui risultato è pari a 24
Posso procedere alla verifica del risultato della media mediante la seguente formula
=SOMMA(E2:E25)/CONTA.NUMERI(E2:E25) il cui risultato è pari ad € 119,42 e coincide il precedente calcolo della media aritmetica.
INTERNALITÀ DELLA MEDIA ARITMETICA
Una delle principali caratteristiche della media aritmetica è quella delle INTERNALITÀ. Il valore della media è sempre compreso tra il minimo ed il massimo dei valori appartenenti all’insieme di calcolo.
Possiamo verificare la precedente affermazione utilizzando le funzioni di MINIMO e MASSIMO.
=MAX(E2:E25) il cui risultato è pari ad € 150,00
=MIN(E2:E25) il cui risultato è pari ad € 90,00
Effettivamente il valore della media aritmetica pari ad € 119,42 è compreso tra i due valori di minimo e di massimo.
TRASFERIBILITÀ DELLA MEDIA ARITMETICA
Si parla di TRASFERIBILITÀ’ della media aritmetica quando si dice che sostituendo il valore della media a quello delle singole determinazioni, il risultato non cambia. Lo possiamo dimostrare con la seguente equazione
=MEDIA(E2:E25)*CONTA.NUMERI(E2:E25)=SOMMA(E2:E25) il cui risultato è pari a VERO
MEDIA ARITMETICA COME BARICENTRO DELL’INSIEME DEI VALORI
Sarà divertente verificare anche un’altra proprietà della media aritmetica, ovvero il BARICENTRO: se sommiamo tutti gli scarti prodotti tra i singoli valori e la media dell’insieme, la loro somma sarà pari a 0.
Potremmo verificare il risultato con una formula matriciale, ma questo tipo di formule verranno introdotte in altri articoli del nostro percorso. Per il momento risolviamo la nostra verifica aggiungendo una colonna alla nostra tabella in cui calcoliamo le singole differenze tra gli elementi dell’insieme e la loro media: gli SCARTI. Nel nostro esercizio esiste una infinitesimale approssimazione di calcolo praticata da Excel che disturba il valore di verifica se si considerano più di 12 decimali. Useremo quindi la seguente formula:
=TRONCA(SOMMA(F2:F25);12) il cui valore è pari a 0

MEDIANA
Dopo aver scoperto la MEDIA ARITMETICA ed alcune delle sue proprietà, continuiamo il nostro viaggio analizzando l’altro indice di posizione della statistica descrittiva, la MEDIANA. Si tratta di un indice che, dati i valori numerici di un insieme ordinati in modo crescente, determina quali di questi sia in una posizione centrale della serie crescente e che abbia lo stesso numero di valori “sotto” e “sopra”.
Nel nostro esempio possiamo calcolare la MEDIANA per gli IMPORTI. Si deve procedere all’ordinamento delle righe in base alla colonna E, quella degli IMPORTI.
Prima di procedere all’ordinamento aggiungo una colonna che identifichi le vendite prima di riordinarle

Per ordinare la matrice selezioniamo l’intervallo A1:G25 e clicchiamo sul pulsante ordina della scheda DATI e seleziono poi come criterio di ordinamento il campo IMPORTO in modo crescente.

Il risultato dell’ordinamento sarà il seguente:

La colonna ID mi permetterà in qualsiasi momento di tornare alla distribuzione di valori iniziale (alla fine della lettura, per esercizio, provate a riordinare il file utilizzando il campi ID… è probabile che troverete alcune simpatiche difficoltà da superare…)
Utilizziamo adesso la funzione MEDIANA di Excel, scrivendo:
=MEDIANA(E2:E25) il cui risultato è PARI ad € 119,50
Abbiamo identificato il valore di mediana ma se controlliamo la nostra colonna “E” non troviamo un tale valore. La spiegazione risiede nel fatto che la mediana di un insieme pari di valori è pari alla semisomma dei “due” valori centrali della serie ordinata. Nel nostro caso Excel ha effettuato la media tra il valore 119 ed il valore 120 presenti rispettivamente in riga 12 e 13 della nostra matrice. Attenzione al fatto che si contano le righe della matrice selezionata e non del foglio di Excel. La nostra matrice ha la prima riga in quella che è la seconda del foglio di calcolo. Le righe sono colorate a manualmente, rinunciando alla FORMATTAZIONE CONDIZIONALE BASATA SU FORMULE.
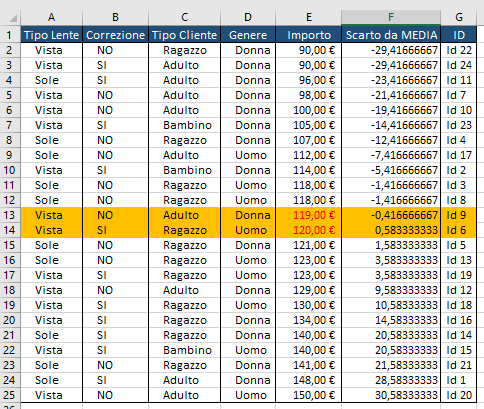
Possiamo usare questa caratteristica della funzione MEDIANA per eseguire una verifica manuale come abbiamo fatto per la MEDIA. Abbiamo compreso che per la MEDIANA abbiamo bisogno di un elenco ordinato di valori e del loro INDICE DI RIGA. Possiamo aggiungere, per comodità, una colonna in cui viene riportato il numero di riga del valore. Utilizziamo la formula
=RIF.RIGA(E2)-1 poiché le righe della nostra matrice sono sfalsate di una posizione nei confronti del foglio

Per poter svolgere manualmente il calcolo della MEDIANA è determinante conoscere se il numero dei valori presenti nell’insieme è pari o dispari. Possiamo dire che se il numero dei valori diviso per due non ha resto, allora sono un numero pari, diversamente sono dispari. Utilizziamo la funzione SE e la funzione RESTO nella cella E35:
=SE(RESTO(CONTA.NUMERI(E2:E25);2)=0;”PARI”;”DISPARI”) che darà PARI come risultato

Dato che le righe sono in numero PARI la MEDIANA sarà la semisomma del valore presente in riga 12 e riga 13 ed in colonna E.
Come possiamo prendere i due valori in modo automatico e dipendentemente che il numero dei valori sia PARI o DISPARI? Utilizziamo la funzione seguente:
=SE(E35=”PARI”;(INDICE(E2:E25;E31/2)+INDICE(E2:E25;E31/2)+1)/2;INDICE(E2:E25;INT(E31/2)+1))
In sintesi la funzione appena descritta ragiona nel modo che segue: se il numero di valori sono PARI effettua la semisomma tra i due valori centrali, mentre se sono DISPARI prende soltanto il valore centrale
MODA
L’ultimo indice di posizione che esaminiamo è la MODA
La moda ci dice qual è il valore dell’insieme che ha la maggiore frequenza e che quindi si ripete più volte.
Nel nostro esempio possiamo adesso lavorare su dei valori qualitativi e sulle loro frequenze. Useremo la funzione CONTA.SE per identificare quante volte sono stati venduti gli occhiali ai tre diversi soggetti acquirenti: Bambino, Ragazzo, Adulto. Scriviamo, in L2, la seguente formula per calcolare la frequenza delle vendite ai diversi tipi di cliente:
=CONTA.SE($C$2:$C$25;K2)
Copieremo verso il basso la formula in modo che copra i tre possibili clienti. Otterremo così quanto in figura: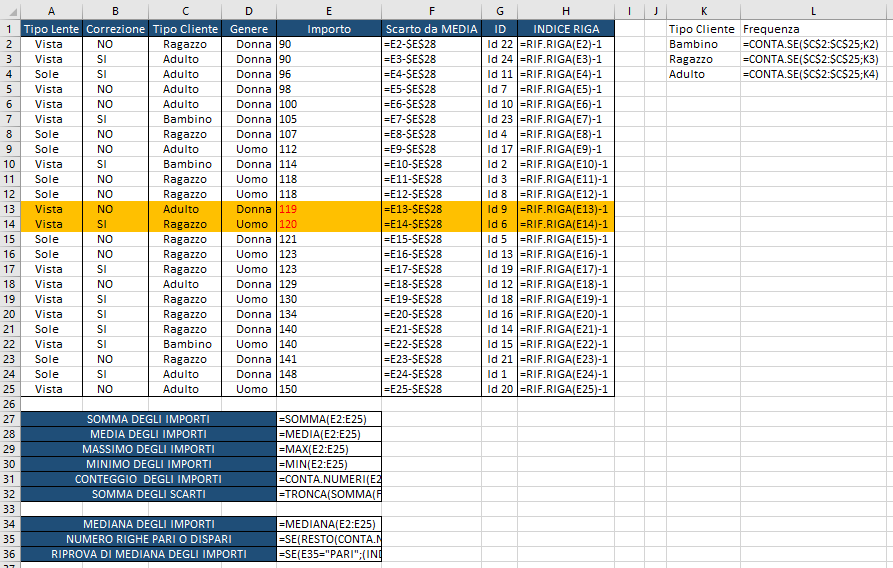
Il valore massimo presente nell’intervallo L2:L4 rappresenta la MODA delle vendite per tipo cliente.

Esaminando i valori presenti in L2:L4 si intuisce come la MODA a cui è riferito il tipo cliente Ragazzo.
Quale formula potrebbe restituire in modo automatico il valore descrittivo associabile al valore di MODA?
Per rispondere dobbiamo usare la funzione CONFRONTA e la funzione INDICE.
La funzione CONFRONTA restituisce il numero di riga di una matrice selezionata che contiene il valore selezionato: se cercassimo il valore 12 in L2:L4 lo troveremmo in seconda riga.
La funzione INDICE restituisce il valore presente in una certa posizione, nel nostro caso la riga, di una matrice.
Esaminando la matrice K2:L4 il Tipo Cliente abbinato al valore di moda si trova nella seconda riga della colonna K.
Il valore di riga viene determinato dalla seguente formula:
=CONFRONTA(E38;L2:L4) che restituisce un valore pari a 2
La voce descrittiva da abbinare al valore di MODA si trova quindi sulla riga 2 appena individuata, ma nella colonna K. Preleveremo tale voce con la seguente formula:
=INDICE(K2:K4;CONFRONTA(E38;L2:L4)
Come per la MEDIANA esiste anche la funzione MODA, ma possiamo utilizzarla solo per i valori numerici. Se per esempio volessimo determinare qual è l’importo di vendita più frequente, potremmo utilizzare la funzione di MODA scritta nel modo seguente:
=MODA(E2:E25) che restituisce un risultato pari a 90
È importante notare come questa funzione non tiene in considerazione le distribuzioni di dati MULTIMODALI. Per questa casistica ci si deve appoggiare ad una funzione che si chiama MODA.MULT e che rientra nelle funzioni matriciali che affronteremo più avanti.
MEDIA, MEDIANA E MODA. QUALE SCEGLIERE?
Non si può dire a priori quale degli indici esaminati possa essere migliore degli altri. La pratica più idonea consiste nel calcolarli tutti per poi fare alcune riflessioni.
Prendiamo per esempio il seguente insieme di dati: 2,3,3,4,5,6,7,8,9,100.
Se ne calcoliamo la media aritmetica dei valori espressi si ottiene un risultato pari a 14,7. Ci si rende immediatamente conto che dei 10 numeri analizzati, 9 sono sotto la media aritmetica. E’ facile intuire che la media aritmetica non è per niente rappresentativo della serie.
La mediana della serie dei valori è invece pari a 5,5 e ci sembra un valore assolutamente più rappresentativo della serie di numeri espressa.
La media aritmetica è troppo spesso influenzata da “valori anomali”.
Se fossimo dei commercianti, molto probabilmente, ci interesserebbe sapere qual è il numero “più venduto” (supponendo, per assurdo, che si possano vendere i numeri!). Nel nostro caso il numero “che va più di moda” è il numero 3; è infatti l’unico numero “venduto” due volte.


